Lab 4 - PID Control

Introduction:

The main objective of this lab was to gain familiarity with controlled actuation and path-following using PID control by understanding the behaviour exhibited by each parameter.

Before starting any of the assessments, I noticed that precisely adjusting the PID values using the control knobs was awkward. The sketch contained code to increment these values through key presses, but these changes were not reflected on the UI. I added a few lines of code in the KeyPress() event to fix this issue, and the result made tuning the parameters much easier. Secondly, I was unable to perform any assessment with the end-effector's star-shaped "head", as the magnet on which it sits was unable to stick to my Haply.

The code for this lab can be found here.

1) Run the code and try out the P controller. How does it feel? What happens when you change the target position? What does changing the P parameter do? Do you notice any problems?

Snapping to the original target position:

With the P value set to 0.01, the Haply’s end-effector did not attempt to “snap” to the target position regardless of how close I brought the device to the target position. I felt a "virtual radial boundary" at a short distance from the target. I could apply a perturbation to the end-effector without feeling any resistive force within this boundary, but felt a resistive force as I attempted to “cross it” with a minor push. I was able to cross the virtual boundary with a larger perturbation, however, but the end-effector successfully managed to snap back to the target once this force, or my hand, was released.

By increasing the P value to 0.02, the end-effector was able to snap to the target position from close to the initial position, but stopped a few units away from the target (i.e., there seemed to be a steady-state error). I felt the same “virtual radial boundary effect”, but this time with the boundary closer to the target. Interestingly, unlike the P = 0.01 case, the end-effector struggled to return to the target position if I tried to cross the boundary with a large perturbation, both on the sketch screen and Haply plate. It would snap to some random position somewhat close to the target instead, forcing me to reset the sketch to resume debugging. As the P value gradually increased, the end-effector could snap to the target position more accurately, and the boundary wall radius seemed to gradually decrease. Thus, at higher P values, the Haply would resist even the most minor pushes with a greater force. When the P value was relatively large (approximately 0.10 or higher), the end-effector was unable to snap to the target position unless I applied damping by gently grasping the end-effector with my hand. It would otherwise vibrate and/or oscillate erratically over a large distance on the Haply plate. This instability was also noticeable when I tried to cross the virtual boundary. Some experimentation with the P parameter can be seen in the video below:

Snapping when the target position is shifted:

At P = 0.01, the end-effector seemed to navigate best to new target positions that were further away, and what I believe were points outside of the virtual radial boundary. It did not move if the new target position was close to the previous one. This was not the close with P = 0.02 where the end-effector could also navigate to nearby points. P = 0.03 exhibited some instability, and this became increasingly noticeable as the value increased. 

The random position generation range of (-0.5, 0.5) for the y-axis led to the end-effector sometimes being pushed off the edge for distant points, so I lowered this range to (-0.5, 0.1) to cover an area closer to the initial position of the joint.

 As with the previous part, damping significantly helped mitigate this instability. A P value of ~0.10 with the user lightly grasping the end-effector seems to work best for navigation; this matches with our observations during iteration 2 of our project, where navigating to a particular data point in a scatter plot seemed smoothest with this configuration.

2) Add the D component to your controller. Tip: You can use a high smoothing (close to 1) to better see the effect of the derivative filter when manually moving the handle, but this adds delay and should be reduced for improving the stability. How does this change the behaviour of the Haply? Are there any problems?

Based on my understanding of the theory, the D parameter stiffens the “spring” to allow for a smoother "landing" at the target position, thus reducing instability as the end-effector moves from point to point. I first wanted to check whether and what value of D could mitigate the large instability issues I faced at high values of P (> 0.03 with no damping). I experimented with a P value of 0.06, roughly halfway between the first unstable and last stable P value I had observed (0.03 – 0.10).

The D value does not seem to be as sensitive as the P, i.e., larger changes in D are required to produce noticeable changes in reducing the instability. I first noticed this at D ~= 0.20, where the end-effector would oscillate only a few times before landing at the target point. At D values close to 1.00, there were little to no oscillations, even for higher values of P. Larger values of D resulted in a high number of low-frequency oscillations. Setting the exponential filter to 1 sometimes removed these vibrations, but the instability persisted.

3) Add the I component to your controller. How does this change the behaviour of the Haply? Can you create a stable system that reaches the target?

Based on my understanding of control theory, the I parameter is meant to correct the trajectory of the end-effector should it overshoot the target point. Similar to the P parameter, it seems to be sensitive to slight changes and that relatively large values (I >= 0.05) often caused instabilities in the system when moving from point to point. A value of 0.02 seemed to work well in minimizing these oscillations while still allowing the end-effector to correct its path, though at times it would take several seconds to reach the target (increasing settling time, based on theory). Based on my observations, the I parameter seems to improve accuracy in that it attempts to move the end-effector to the exact center of the target via “micro adjustments”, minimizing the steady-state error completely, which was clear from observing the sketch window; the PD controller, in contrast, would simply navigate “close enough” to the target.

4) Implement path tracking, specifically, replace the random position by a position following a track over time (e.g., a circle or square). What happens when you old the handle ? How is it affected by the PID parameters?

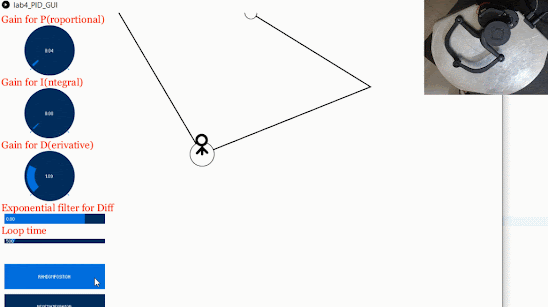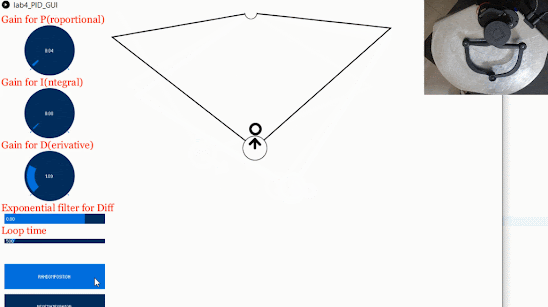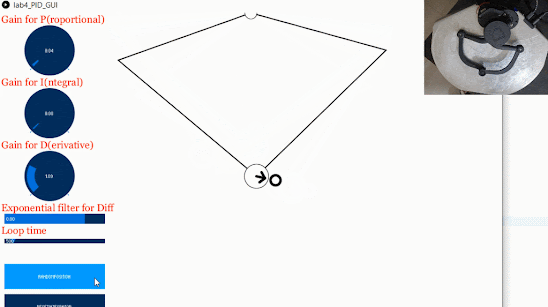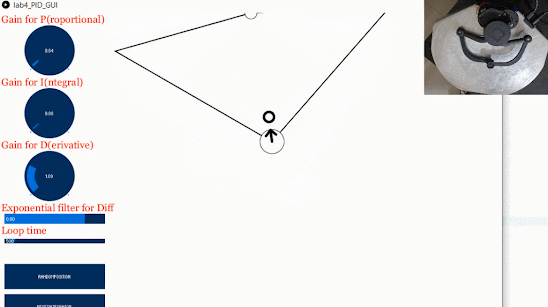
For this assessment, I experimented with the PID parameters using two types of paths: a square, and a circle. To trace a square, movement is required in one-direction at a time. For a circle, movement occurs in two directions simultaneously. I wondered whether the tracking accuracy would be worse in the latter case. The code to generate a square is based off this code, while the equation of a circle is used to generate the circular path. The trajectories can be observed by uncommenting out either line 443 or 444 in the Processing code. The “speed” is varied by modifying the rate of change of position per loop in the simulation thread. I decided to only vary the P value and speed at first.

For the circle, the path tracking was smooth for values of P up to approximately 0.30 for low speeds. Unsurprisingly, higher P values in this range would cause instability at higher speeds and the value would have to be reduced to approximately 0.05-0.10 to maintain stability.

There did not seem to be any noticeable difference with the square-tracking path. Similar P values and speeds yielded similar results.

Video showing the effect of P values at low speeds for the square trajectory:

Video showing the effect of P values at high speeds for the square trajectory:

You can see how a rhombus-like trace is left on the Haply plate after running the path tracking for several minutes (this was from the circular trajectory):

Interestingly, the D and I parameters seemed to adversely affected the end-effector’s movement. Relatively low or medium values of D (0.00 - 1.00), regardless of the path or end-effector movement speed, did not cause instability but generated low frequency vibrations that caused jerkier movement of the end-effector. These vibrations were more frequent at higher values of D (> 2.00).

Any value of I “broke” the end-effector’s path-following ability, regardless of the P value or speed. Thus, it seemed that only tuning the P parameter seemed to provide the most accurate results in both the square and circle trajectories.

Holding the handle allows for stability at higher P values due to the applied damping effect. The more firmly the end-effector is held, the higher the damping and thus the higher the resistive force applied, slowing down the end-effector’s motion. Given that both paths are position-based trajectories, the end-effector still continues to complete the paths, only taking longer durations to do so.

An interesting observation: the end-effector would become unstable after running the path-tracking for several minutes for generally stable values of P and speed. Could this be due to increased friction in the linkages after minutes of continuous motion?

5) Play with the controller update rates, and with introducing delays. Hint: use the “looptime” parameter. How does this change the system? What happens if you sample faster or slower? What happens if it’s random (this would require some coding)?

I tested changes in the looptime parameter with the path tracking assessment. A higher loop time seems to result in slower and jerkier movement, with extremely high values (> 3500) gradually resulting in instability from oscillatory motion. This is likely due to “sudden” changes in the cumulative error arising from a lower sampling rate. Conversely, the motion appears to be slightly smoother with a lower loop time value of 250.

A random loop time value was set by adding the following code inside the while loop of the simulation thread (lines 407-408 in the code):

    looptime = int(random(100, 3000));

    cp5.getController("looptime").setValue(looptime);

Where the two parameters of the random function denote the minimum and maximum possible loop time values. Generally speaking, the movement seemed to vary from smooth to jerky, especially at faster path-following speeds. The end-effector would inevitably become unstable, likely from hitting one of the higher looptime values.

Reflections:

I enjoyed the first couple of assessments of this lab – and it was fascinating to observe the PID “snapping” effect and autonomous movement – but the lab become a bit tiring as it contained the type of work I had mentioned I would dislike in my lab 2 blog post: repeatedly tuning several parameters from trial and error, and recompiling the code to observe and note changes. This was exacerbated by the need to constantly reset the simulation and occasionally the Haply motor switch whenever the system became unstable. However, at the same time, I think that’s the crux of the “PID problem” – figuring out what works best for the system by simulating the code with several combinations of the parameters until the desired result is achieved; this lab made me realize that that can take a lot of time and effort. I also initially feared the Haply might break from the unstable behavior under certain conditions but later developed a trust on its robustness after running several sketches. However, care should still be taken as repeated instability could lead to fatigue in the mechanical components of the device. In any case, I gained a good feel for the behavior exhibited by each of the PID parameters with all of the hands-on experimentation, which was a significant learning experience! The quick navigation and autonomous path movement inspired us for the second iteration of our project, where a user can quickly snap to a particular data point on a scatter plot.